Okedra simetrio
La regula okedro havas turnan simetrion de ordo 24 (kiu inkluzivas turnajn transformojn sed ne inkluzivas reflektajn transformojn), kaj entutan simetrion de ordo 48 (kiu inkluzivas kaj reflektajn kaj turnajn transformojn). Kubo havas la samajn simetriojn pro tio ke ĝi estas la duala pluredro de okedro.
La grupo de orientiĝo-konservantaj simetrioj estas S4, aŭ la grupo de permutoj de kvar objektoj, pro tio ke estas akurate unu tia simetrio por ĉiu permuto de la kvar paroj de kontraŭaj edroj de la okedro.
Turna okedra simetrio kaj plena okedra simetrio estas la diskretaj punktaj simetrioj (aŭ ekvivalente, simetrioj sur sfero) kun la plej grandaj geometriaj simetriaj grupoj kongruaj kun mova simetrio. Ili estas en la kristalaj punktaj grupoj de la kuba kristala sistemo.
Turna okedra simetrio
[redakti | redakti fonton]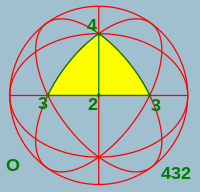
O, 432, aŭ de ordo 24, estas turna okedra simetrio . Ĉi tiu grupo estas simile al turna kvaredra simetrio T, sed la C2 aksoj estas en la okedra turna simetrio C4 aksoj, kaj aldone estas 6 C2 aksoj tra la mezpunktoj de lateroj de la kubo. Td kaj O estas izomorfiaj kiel abstraktaj grupoj: ili ambaŭ esti konforma laŭ S4, la simetria grupo je 4 objektoj. Td estas la unio de T kaj la aro ricevita per komponado de ĉiu ero de O \ T kun la inversigo. O estas la turna grupo de la kubo kaj de la regula okedro.
Plena okedra simetrio
[redakti | redakti fonton]


- Oh (*432) de ordo 48 estas plena okedra simetrio. Ĉi tiu grupo havas la samajn turnajn aksojn kiel O, sed kun spegulaj ebenoj, kiuj estas la spegulaj ebenoj de ambaŭ Td kaj Th. Ĉi tiu grupo estas izomorfia al S4 × C2, kaj estas la plena geometria simetria grupo de la kubo kaj okedro.
Kun la 4-oblaj aksoj koincidantaj kun la koordinataj aksoj, fundamenta domajno de Oh estas donita per kondiĉo 0 ≤ x ≤ y ≤ z. Objekto kun ĉi tiu simetrio estas karakterizita per la parto de la objekto en la fundamenta domajno, ekzemple la kubo estas donita per z ≤ 1 (z = 1 por la rando) , kaj la okedro per x + y + z ≤ 1 (x + y + z = 1 por la rando). ax + by + cz = 1 donas randon de pluredro kun 48 edroj, la piramidigitan dekduedron.
La edroj estas kombinataj po 8 al pli grandaj edroj por a = b = 0 por kubo, kaj kombinataj po 6 por a = b = c por okedro.
Konjugecaj klasoj
[redakti | redakti fonton]La konjugecaj klasoj de O estas:
- idento
- 6 × turno je 90°
- 8 × turno je 120°
- 3 × turno je 180° ĉirkaŭ 4-obla akso
- 6 × turno je 180° ĉirkaŭ 2-obla akso
Tiuj de Oh inkluzivas ankaŭ tiujn kun inversigo:
- inversigo
- 6 × turnoreflekto je 90°
- 8 × turnoreflekto je 60°
- 3 × reflekto de ebeno perpendikulara al 4-obla akso
- 6 × reflekto de ebeno perpendikulara al 2-obla akso
Iuj nememspegulsimetriaj pluredroj kun turna okedra simetrio
[redakti | redakti fonton]| Nomo | Speco | Bildo | Edroj | Lateroj | Verticoj | |
|---|---|---|---|---|---|---|
| Mallaŭ horloĝa nadlo | Laŭ horloĝa nadlo | |||||
| Riproĉa kubo | Arĥimeda solido | 
|

|
38 | 60 | 24 |
| Kvinlatera dudekkvaredro | Katalana solido | 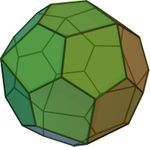
|

|
24 | 60 | 38 |
Iuj pluredroj kun plena okedra simetrio
[redakti | redakti fonton]| Nomo | Speco | Bildo | Edroj | Lateroj | Verticoj | |
|---|---|---|---|---|---|---|
| Kubo | Platona solido | 
|
6 | 12 | 8 | |
| Okedro | Platona solido | 
|
8 | 12 | 6 | |
| Kubokedro | Arĥimeda solido, kvazaŭregula pluredro | 
|
14 | 24 | 12 | |
| Senpintigita kubo | Arĥimeda solido | 
|
14 | 36 | 24 | |
| Senpintigita okedro | Arĥimeda solido | 
|
14 | 36 | 24 | |
| Malgranda rombokub-okedro | Arĥimeda solido | 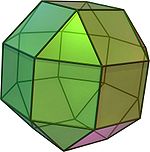
|
26 | 8 trianguloj 18 kvadratoj |
48 | 24 |
| Granda rombokub-okedro | Arĥimeda solido | 
|
26 | 72 | 48 | |
| Romba dekduedro | Katalana solido, duala de kvazaŭregula pluredro | 
|
12 | 24 | 14 | |
| Trilateropiramidigita okedro | Katalana solido | 
|
24 | 36 | 14 | |
| Stelokangulopluredro | 
|
8 | 12 | 8 | ||
| Kvarlateropiramidigita kubo | Katalana solido | 
|
24 | 36 | 14 | |
| Deltosimila dudekkvaredro | Katalana solido | 
|
24 | 48 | 26 | |
| Piramidigita dekduedro (seslateropiramidigita okedro) |
Katalana solido | 
|
48 | 72 | 26 |

