Reto (pluredro)

En geometrio, reto de pluredro estas ebena figuro, konsistanta el edraj plurlateroj de la pluredro, kunigitaj je parto de la lateroj en tiu ordigo ke ĝi povas esti faldita (laŭ la lateroj) kaj iĝi la edrojn de la pluredro en 3-dimensia spaco.
Modelo de pluredro povas esti konstruita el materialo simila al kartono en formo de la reto kaj poste faldita.
Estas delonge staranta malfermita problemo ĉu ĉiu konveksa pluredro P (do, kun ĉiuj duedraj anguloj je lateroj ne pli grandaj ol π) havas reton kiu povas esti en ebeno sen interkovroj. Alivorte, ĉu la surfaco de P povas esti tranĉita laŭ parto de la lateroj kaj malfaldita en ebena plurlateron sen interkovroj. La problemo estis unua eksplicite priskribita en papero de Shephard. [1] La historio kaj progreso de la problemo estas diskutita en parto III de Geometriaj faldaj algoritmoj [2].
Ankaŭ, la plej mallonga vojo sur la surfaco inter du punktoj sur la surfaco de pluredro korespondas al rekto sur taŭga reto. La reto devas esti tia ke la rekto estas plene en ĝi, kaj oni povas devi konsideri kelkajn retojn poe vidi kiu donas la plej mallongan vojon. Ekzemple, ĉe kubo, se la punktoj estas sur najbaraj edroj unu kandidato por la plej mallonga vojo estas la vojo krucanta la komuna lateron; la plej mallonga vojo de ĉi tiu speco estas trovata uzante reton kie la du edroj estas najbara. Aliaj kandidatoj por la plej mallonga vojo estas tra surfaco de la tria edro najbara al ambaŭ la fontaj, kaj respektivaj retoj povas esti uzataj por trovi la plej mallongan vojon el ĉi tiuj.
Reto de hiperpluredro en pli altaj dimensioj
[redakti | redakti fonton]En pli altaj dimensioj reto de n-dimensia hiperpluredro estas (n-1)-dimensia figuro, konsistanta el facetoj de la hiperpluredro, kunigitaj je parto de la krestoj en tiu ordigo ke ĝi povas esti faldita (laŭ la krestoj) kaj iĝi la facetojn de la hiperpluredro en n-dimensia spaco.
Ekzemple, reto de plurĉelo, aŭ kvar-dimensia hiperpluredro, estas komponita el pluredraj ĉeloj kiuj estas koneksa laŭ iliaj edroj kaj ĉiuj kuŝas en la sama tri-dimensia spaco.
 4-hiperkubo |
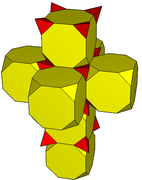 Senpintigita 4-hiperkubo |
 24-ĉelo |
Referencoj
[redakti | redakti fonton]- ↑ Geoffrey Shephard (1975). Konveksaj hiperpluredroj kun konveksaj retoj. Math. Proc. Camb. Phil. Soc. 78 389-403. ISSN 1469-8064.
- ↑ Erik Demaine & Joseph O'Rourke. (Julio 2007) Geometric Folding Algorithms: Linkages, Origami, Polyhedra (angle). Cambridge University Press. ISBN 978-0-521-85757-4.
Eksteraj ligiloj
[redakti | redakti fonton]- Eric W. Weisstein, Reto en MathWorld.
- Retoj: ilo por prezenti pluredrojn en du dimensioj
- Pri retoj
- Malfoldaĵoj de regula 4d hiperpluredroj Arkivigite je 2011-07-17 per la retarkivo Wayback Machine
