Elektromagneta radiado

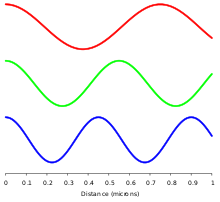
Elektromagneta ondo: ligita oscilado de elektra kampo kaj magneta indukdenso, modelo de vibranta dupoluso, norma 3-dimensia sistemo de karteziaj koordinatoj: (${\vec {v}}$,${\vec {E}}$,${\vec {B}}$)

Elektromagneta radiado estas radiado el elektra kampo (${\vec {E}}$) kaj magneta indukdenso (${\vec {B}}$) de fotonoj. La du kampoj estas ortaj inter si kaj havas fiksan rilaton.

Oni montras la relativajn ondolongojn de la elektromagnetaj ondoj de tri diferencaj koloroj de lumo (blua, verda kaj ruĝa) kun distanca skalo en mikrometroj laŭlonge de la ikso-akso.

La fizikisto James Clerk Maxwell en 1864 antaŭdiris elektromagnetajn ondojn surbaze de teoriaj kalkuloj kaj la ekvacioj poste nomitaj laŭ li. Li kalkulis, ke ili propagiĝas per lumrapido kaj tial jam (prave) supozis, ke videbla lumo konsistas el elektromagnetaj ondoj. En 1888 Heinrich Rudolf Hertz praktike demonstris la ekziston de elektromagnetaj ondoj.

Parto de videbla spektro

Elektromagnetaj ondoj havas diversajn frekvencojn ( f ), ligitajn al la ondolongo (λ) per la lumrapido c ( f·λ = c ). La rapido de iliaj fotonoj ne varias laŭ la moviĝo de la mezursistemo, sed estas absoluta kaj konstanta. Tiun fakton Albert Einstein eltrovis en sia speciala teorio de relativeco.

Elektromagnetaj ondoj montras fenomenojn, kiuj klare distingas ilin kiel ondojn, ekzemple interferon. Aliflanke ili montras ankaŭ fenomenojn, kiuj pruvas ilian partiklan naturon, ekzemple la fakton (lasero), ke la joniga kapablo de lumo dependas ne de ties intenso, sed de ties frekvenco. Elektromagnetaj ondoj do klare montras duoblan naturon, kaj sin tenas kiel ondoj kaj partikloj.

Aparatoj

Diagramo de bolometro.

Bolometro estas aparato, kiu mezuras la varmigan povumon de elektromagneta radiado. Bolometro konsistas el du ĉefelementoj:

• Varmosorbilo, ekzemple maldika metala lado
• Varmorezervujo (korpo tiel granda, ke ĝia temperaturo ne multe ŝanĝas)

La du elementoj estas ligitaj per varmokonduktilo.

Kiam radioj verŝiĝas sur la sorbilon, la sorbilo varmiĝas. La varmo trafluas tra la kondukilo en la rezervujon. Se la rapido de radia surverŝo estas sufiĉe granda, do la sorbilo hejtiĝas pli rapide ol la kapablo de la kondukilo forkondukti la troan varmon; termometro (ekz. termistoro) povas do mezuri la temperaturan diferencon inter la du ĉefelementojn kaj, tiele, la radian povumon.

Se la varmokapacito de la sorbilo estas $C$ (en ĵulo/kelvino), kaj la varmokonduktanco de la konduktilo estas $G$ (en vato/kelvino), do la tempa varmokonstanto estas $\tau =C/G$ (en sekundo). Ju pli granda estas la tempa varmokonstanto, des pli sentiva estas la bolometro.

Historio de rilataj malkovroj

Benjamin Franklin ĉirkaŭ la jaro 1750 esploradis elektrostatikon. Multaj tiamaj fizikistoj ekkonatiĝis kaj interesiĝis pri elektro, danke al liaj eksperimentoj pri fulmoj kaj iliaj proprecoj.

Franklin publikigis hipotezon, laŭ kiu elektrajn proprecojn kaŭzis iu elektra likvaĵo per sia abundo aŭ malabundo en materialoj. Kvankam malĝusta, lia teorio komencis la ĝisnunan kutimon uzi la simbolojn + kaj - por priskribi elektrajn ŝarĝojn.

Kulombo.

En la jaro 1785, Charles-Augustin de Coulomb verkis tri memuarojn pri elektro kaj magnetismo, en kiu li raportis, ke la forto inter du elektraj ŝargoj estas simila al la gravito, kaj ke la forto estas inverse proporcia al la kvadrato de la rekta distanco inter la partikloj, la ŝargo de ili estas proporcia al iliaj densecoj de elektra fluidaĵo. La vektora formulado de la kulomba leĝo laŭ la internacia sistemo de unuoj estas:

${\vec {\mathbf {F} }}_{12}=q_{1}{\vec {\mathbf {E} }}_{2}={\frac {1}{4\pi \epsilon _{0}}}{q_{1}q_{2} \over r^{2}}\,\mathbf {\hat {r}} _{21}\ ,$

kie

${\vec {\mathbf {F} }}_{12}$ estas la elektra forto inter la partiklo 1 kaj la partiklo 2,

${\vec {\mathbf {E} }}_{2}$ estas la elektra kampo de la partikulo 2, en la loko de la partiklo 1,

q₁ et q₂ estas la respektivaj elektraj ŝargoj de la partikloj 1 et 2,

$r=|{\vec {\mathbf {r} }}_{1}-{\vec {\mathbf {r} }}_{2}|$ estas la distanco inter la partikloj 1 kaj 2, t.e.

$\mathbf {\hat {r}} _{21}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {{\vec {\mathbf {r} }}_{1}-{\vec {\mathbf {r} }}_{2}}{\vert {\vec {\mathbf {r} }}_{1}-{\vec {\mathbf {r} }}_{2}\vert }}$ estas vektoro indikanta la direkton de la forto suferita de partiklo 1 fare de partiklo 2, kaj

${\frac {1}{4\pi \epsilon _{o}}}=8.988\times 10^{9}\,[{\frac {Nm^{2}}{C^{2}}}]$ estas elektra konstanto, foje nomata kulomba konstanto.

Gaŭso.

Johann Carl Friedrich Gauss, matematikisto kaj sciencisto, en la jaro 1813, formulis la teoremon pri la inversa kvadrata leĝo de kampoj, kaj deduktis sian gaŭsan leĝon, kiu poste konsideriĝis kiel aparta kazo de la nuna nomita teoremo de Stokes. Aplikante la gaŭsan leĝon oni deduktas la kulomban leĝon, kaj per la diverĝenca teoremo (foje ankaŭ nomita gaŭsa teoremo) oni obtenas la gaŭsan elektrostatikan formulon sub la diferenciala formo de hodiaŭ:

$\nabla \cdot {\vec {\mathbf {E} }}=\rho /\epsilon _{o}\,,$

kie $\nabla \cdot$ estas la diverĝenco, $\rho$ estas la loka denso de elektra ŝargo ĉirkaŭ la konsiderita punkto, se estas pluraj elektre ŝargitaj partikloj en iu volumeno, sekve ke ${\vec {\mathbf {E} }}$ estas la rezulta elektra kampo kreita de tiuj partikloj.

Nigrakorpa radiado

Nigra-korpa radiado estas la varma elektromagneta radiado ene, aŭ ĉirkaŭ, korpo en termodinamika ekvilibro kun sia medio, elsendita de nigra korpo (idealigita netravidebla, nereflekta korpo). Ĝi havas specifan, kontinuan spektron de ondolongoj, inverse rilataj al intenseco, kiu dependas nur el la korpa temperaturo, kio estas akceptita, je konto de kalkuloj kaj teorio, kiel uniforma kaj konstanta.

Dum la temperaturo de nigra korpo malpliiĝas, ankaŭ ties intenseco malpliiĝas kaj ties pinto moviĝas al pli longaj ondolongoj.

Max Planck

En 1894, Max Planck turnis sian atenton al la problemo de la nigra-korpa radiado. Tiu problemo estis jam starigita de Kirchhoff en 1859: "kiel la intenseco de la elektromagneta radiado elsendita de nigra korpo (perfekta absorbanto, konata ankaŭ kiel kavaĵa radianto) dependas el la frekvenco de la radiado (t.e., la koloro de la lumo) kaj el la temperaturo de la korpo?". La demando estis esplorita eksperimente, sed neniu teoria traktado kongruis kun la eksperimentaj valoroj. Wilhelm Wien proponis la leĝon de Wien, kiu ĝuste antaŭdiris la kutimaron je altaj frekvencoj, sed malsukcesis je malaltaj frekvencoj. La Leĝo Rayleigh–Jeans, nome alia alproksimiĝo al la problemo, kongruis kun la eksperimentaj rezultoj je malaltaj frekvencoj, sed kreis tion kio estis poste konata kiel la "ultraviola katastrofo" je altaj frekvencoj. Tamen, kontraŭ multaj lernolibroj, tio ne estis motivado por Planck.

Planck reviziis sian unuan alproksimiĝon al la nigra-korpa radiado, fidante al la statistika interpretado fare de Boltzmann de la dua leĝo de termodinamiko kiel vojo akiri pli fundamentan komprenon de la principoj malantaŭ sia radiad-leĝo.

La unua proponita solvo de Planck al la problemo en 1899 sekvis el tio kion Planck nomis la "principo de elementa disordo", kio ebligis, ke li derivu la leĝon de Wien el nombraj supozoj pri la entropio de ideala oscilado, kreante tion kio estis referencita kiel la leĝo Wien–Planck. Tuj oni trovis, ke eksperimenta pruvaro ne konfirmis la novan leĝon entute, ĝis Planck alvenis al frustracio. Planck reviziis sian alproksimiĝon, derivante la unuan version de la fama Leĝo de Planck pri la nigra-korpa radiado, kiu bone priskribis la eksperimente observitan nigra-korpan spektron. Ĝi estis por la unua fojo proponita en kunsido de DPG la 19an de Oktobro 1900 kaj publikigita en 1901. Tiu unua derivaĵo ne inkludis energikvantigon, kaj ne uzis statistikan mekanikon, por kio li sentis malinklinon. En Novembro 1900 Planck reviziis tiun unuan alproksimiĝon, fidante al la statistika interpretado fare de Boltzmann de la dua leĝo de termodinamiko kiel vojo akiri pli fundamentan komprenon de la principoj malantaŭ sia radiad-leĝo. Ĉar Planck estis tre malfidaj de la filozofiaj kaj fizikaj implikoj de tia interpretado de la alproksimiĝo fare de Boltzmann, lia reago estis, kiel li mem poste asertis, "ago de malespero ... Mi estis preta oferi ajnan el miaj antaŭaj konvinkoj pri fiziko".

La centra dedukto malantaŭ lia nova derivaĵo, prezentita al la DPG la 14an de Decembro 1900, estis la supozo, nune konata kiel la postulato de Planck, ke elektromagneta energio povus esti elsendita nur en kvantigita formo, alivorte, la energio povus esti nur multoblo de elementa unuo:

$E=h\nu$

kie h estas la Konstanto de Planck, konata ankaŭ kiel kvantuma agado de Planck (jam enkondukita en 1899), kaj ν estas la frekvenco de la radiado. Oni notu, ke la elementaj unuoj de energio tie studitaj estas reprezentataj per hν kaj ne simple per ν. Fizikistoj nune nomas tiujn kvantumaj fotonoj, kaj fotono de frekvenco ν havos sian propran specifan kaj unikam energion. La totala energio je tiu frekvenco estas tiam egala al hν multobligita per la nombro de fotonoj je tiu frekvenco.

Optika sorbo

Pli detalaj informoj troveblas en artikolo Optika sorbo.

Sorbado de elektromagneta radiado (aŭ en speciala kazo kaj ankaŭ simple dirite Lumosorbado) estas la procezo de perdo de energio per fluo de elektromagneta radiado pro interago kun materio. Ĝi estas fizika interago en kiu lumo liberigas sian energion en materion. Lumo-sorbado estas speciala kazo de la pli ĝenerala fizika fenomeno de sorbado. Kiam elektromagneta radiado estas sorbita, elektrono en atomo iras de energie pli favora stato al stato kun pli alta energio, tio okazas per la "elektronsalto". Tio estas nomita elektronika ekscito. La inversa procezo al lumsorbado estas spontanea lum-emisio. Lumo estas elsendita de materio, per kio la interna energio de la materio malpliiĝas je la responda energiproporcio.

Vidu ankaŭ

• elektromagneta ondo
• fotono
• radioondo
• radiofonio
• mikroondoj
• infraruĝa radiado
• kosma fona radiado
• videbla spektro
• lumo
• ultraviola radiado
• ikso-radioj
• gamo-radioj
• spektra linio
• detektilo

Bibliografio

• Hecht, Eugene. (2001) Optics, 4‑a eldono, Pearson Education. ISBN 978-0-8053-8566-3.
• Kondepudi, D.; Prigogine, I. (1998). Modern Thermodynamics. From Heat Engines to Dissipative Structures. John Wiley & Sons. ISBN 0-471-97393-9.
• Landsberg, P. T. (1990). Thermodynamics and statistical mechanics (Represo). Courier Dover Publications. ISBN 0-486-66493-7.
• Loudon, R. (2000) [1973]. The Quantum Theory of Light (tria eld.). Cambridge University Press. ISBN 0-19-850177-3.
• Mandel, L.; Wolf, E. (1995). Optical Coherence and Quantum Optics. Cambridge University Press. ISBN 0-521-41711-2.
• Serway, Raymond A.. (2004) Physics for Scientists and Engineers, 6‑a eldono, Brooks Cole. ISBN 978-0-534-40842-8.

• Tipler, Paul. (2004) Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics, 5‑a eldono, W. H. Freeman. ISBN 978-0-7167-0810-0.
• Reitz, John. (1992) Foundations of Electromagnetic Theory, 4‑a eldono, Addison Wesley. ISBN 978-0-201-52624-0.

• Jackson, John David. (1999) Classical Electrodynamics, 3‑a eldono, John Wiley & Sons. ISBN 978-0-471-30932-1.
• Allen Taflove kaj Susan C. Hagness. (2005) Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed. Artech House Publishers. ISBN 978-1-58053-832-9.

Eksteraj ligiloj

• OPTIKO Arkivigite je 2006-06-20 per la retarkivo Wayback Machine: Ĉapitro el lernolibro far SÁRKÖZI János. Subĉapitroj: optiko ĝenerale, fotometrado, ekesto, propagiĝo, refrakto de la lumo, ondooptiko, polarigo, lumo kaj materialo, la okuloj, optikaj instrumentoj. 129 paĝoj, formo PDF, 882 KB.
• "Electromagnetism" Arkivigite je 2011-06-03 per la retarkivo Wayback Machine – ĉapitro el reta lernolibro
• Electromagnetic Waves from Maxwell's Equations en Project PHYSNET.
• Radiado def atomoj? e-m ondo, Polusigo, ... Arkivigite je 2010-04-17 per la retarkivo Wayback Machine
• Enkonduko al The Wigner Distribution in Geometric Optics